BAB 9 STATISTIKA (1)

 

BAB 9 STATISTIKA (1)

Tahukah kalian tentang BPS (Badan Pusat Statistik) ? BPS adalah Lembaga Pemerintah non Departemen yang bertanggungjawab melakukan survey statistika (sensus), menyajikan dan menyediakan data untuk Pemerintah dan Lembaga lain. Hasil survey dan analisa data nantinya akan digunakan dasar oleh Pemerintah untuk menentukan kebijakan-kebijakan publik.

Kalau di Pemalang kantornya ada di Jalan Tentara Pelajar Mulyoharjo, sebelah selatan MtsN Pemalang. Silahkan tambah wawasan kalian tentang Lembaga Negara di Pemalang.

Jika kalian berminat berkarier di Bidang ini, kalian bisa merencanakan pendidikan di Pendidikan Tinggi jurusan Statistika atau Sekolah Statistik seperti STIS.

Kali ini kita akan membahas ilmu statistika dari yang paling sederhana.

Kelas 7 kalian telah belajar membuat Diagram, dari mulai diagram batang, diagram garis dan diagram lingkaran. Masih ingat ya caranya?

Sekarang yuk kita upgrade lagi pengetahuan dan keterampilan tentang Statistika

Kali ini kita awali dengan Pengertian dan Membaca, menganalisa Data dan memprediksi berdasarkan data dari tabel atau diagram

A.   Pengertian Statistika

Statistika merupakan suatu cabang dari matematika yang mempelajari bagaimana cara untuk mengumpulkan data, menyusun data, menyajikan data, mengolah sekaligus menganalisis data, menarik kesimpulan, dan juga menafsirkan data.

 

B.   Membaca, menganalisa Data dan memprediksi berdasarkan data dari tabel atau diagram

 

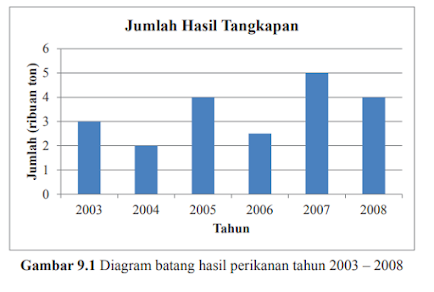
1.    Diagram Batang Hasil Tangkapan Ikan di suatu Daerah Tahun 2003 - 2008

(Buku Paket halaman 227)

Dari diagram di atas dapat kita buat tabel sebagai berikut :

Tahun	Jumlah Hasil Tangkapan
2003	3000 ton
2004	2000 ton
2005	4000 ton
2006	2500 ton
2007	5000 ton
2008	4000 ton

Dari data di atas kita dapat menyimpulkan bahwa :

1.    Hasil tangkapan terendah terjadi pada tahun 2004 yaitu hanya 2000 ton

2.    Hasil tangkapan tertinggi di capai pada tahun 2007 yaitu 5000 ton

3.    Tahun 2003-2004 terjadi penurunan hasil tangkapan sebesar 1000 ton (3000-2000)

Tahun 2004-2005 terjadi kenaikan hasil tangkapan sebesar 2000 ton  (4000-2000)

Tahun 2005-2006 terjadi penurunan hasil tangkapan sebesar 1500 ton  (4000-2500)

Tahun 2006-2007 terjadi kenaikan hasil tangkapan sebesar 2500 ton (5000-2500)

Tahun 2007-2008 terjadi penurunan hasil tangkapan sebesar 1000 ton (5000-4000)

4.    Kenaikan tertinggi di capai pada tahun 2006-2007 yaitu mencapai 2500 ton

5.    Penurunan terbesar terjadi pada tahun 2005-2006 yaitu 1500 ton

6.    Jumlah tangkapan tahun 2004-2008 adalah 25.000 ton (3000+2000+4000+2500+5000+4000)

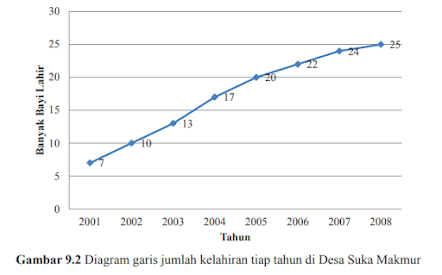
 2.    Diagram Garis Jumlah Kelahiran tiap Tahun di Desa Suka Makmur

(Buku Paket halaman 228)

LATIHAN (Salin dan kerjakan di Buku catatan kalian)

1.    1. Lengkapi tabel berikut

Tahun	Banyak Bayi Lahir
2001
2002
2003
2004
2005
2006
2007
2008

2.    2. Pada tahun berapakah jumlah kelahiran tertinggi ?

3.    3. Pada tahun berapakah jumlah kelahiran terendah ?

4.    4. Berapakah banyak kenaikan kelahiran dari tahun 2001-2002, 2002-2003, 2003-2004, 2005-2006, 2006-2007, dan 2007-2008?

5.    5. Pada tahun berapa terjadi kenaikan kelahiran tertinggi ?

6.    6. Berapakah jumlah kelahiran dari tahun 2001-2008 ?

7.    7. Apa pendapat kalian tentang Program Keluarga Berencana di Desa tersebut ?

 

 

BAB 8 : JAJARGENJANG DAN TRAPESIUM

 BAB 8 : JAJARGENJANG DAN TRAPESIUM

B.  JAJARGENJANG  DAN TRAPESIUM

  Masihkah kalian ingat sifat-sifat jajargenjang dan trapesium ?

Yuuk kita ulang membaca lagi ....

1. Jajargenjang

 Keliling dan Luas Jajargenjang.

Perhatikan contoh-contoh berikut : 

Secara umum, rumus keliling dan luas Jajargenjang, adalah :

Sisi alas tidak selalu berada di bawah. Bisa juga terletak di samping, atau di atas.

2. Trapesium

Jenis-jenis trapesium :

1.    Trapesium sama kaki

2.    Trapesium siku-siku

3.    Trapesium sembarang

 Perhatikan gambar di bawah ini :

Keliling dan Luas Trapesium.

Perhatikan contoh-contoh berikut :

 

Secara umum rumus keliling dan luas trapesium, adalah :

Contoh :

1.    1. Diketahui jajar genjang ABCD dengan AB = 12 cm dan AB : BC = 4 : 3 dengan jika tinggi = 6 cm,

a.     hitunglah luasnya.

b.    hitunglah kelilingnya

 2.    Andi mengelilingi lapangan berbentuk trapesium samakaki sebanyak 10 kali, tinggi               trapesium    12 m dan dua sisi sejajar panjangnya 25 m dan 15 m. Jarak yang ditempuh Andi adalah ......( dengan langkah sbb.)

a.    panjang semua sisi trapesium adalah .......

b.    Keliling trapesium = ......

c.    Jadi jarak yang ditempuh Andi ......

3.             Tentukan luas jajargenjang berikut :

 

Pembahasan 

1.  a . Luas jajar genjang kita gunakan rumus yaitu:

Luas = alas x tinggi

Luas = 12 cm x 6 cm

Luas = 72 cm²

b  Untuk mancari keliling ABCD terlebih dahulu harus mencari panjang BC dengan menggunakan konsep perbandingan, yaitu:

        AB : BC = 4 : 3

12 cm : BC = 4 : 3

            BC = ¾ (12 cm)

            BC = ¾ (12 cm)

            BC = 9 cm

Dengan menggunakan panjang BC kita bisa mencari keliling jajar genjang yaitu:

keliling = 2 (AB+BC)

keliling = 2 (12 cm + 9 cm)

keliling = 2 (21 cm)

keliling = 42 cm

2.    dibuat sketsa trapesium sama kaki lebih dulu :

      AB dan DC adalah sisi yang sejajar. AB = 25 m, DC = 15 m

      Tinggi trapesium = DE = 12 m

      AE = FB maka EF = DC, jadi panjang AE = (25 – 15) : 2 = 5 m.

      Untuk menghitung panjang AD dipakai rumus :

               AD² = AE² + ED²

                     =  5² + 12²

                     =  25 + 144

                     =  169

               AD  = 13 m

a.    jadi panjang sisi trapesium AB = 25 m. BC = AD = 13 m. DC = 15 m

b.    keliling trapesium = 25 + 13 + 15 + 13 = 66 m

c.    Andi mengelilingi lapangan 10 kali.

Jadi jarak yang ditempuh 10 x 66 = 660 m

 

1.    3. Menghitung luas jajargenjang berikut

 Pada gambar  di atas, sisi alas terletak di samping, yaitu VU = 13 cm. Tinggi = 9 cm.

Jadi luas jajargenjang :

  L = alas x tinggi

    =  13 x 9

    =  117 cm²

Demikian penjelasan tentang jajar genjang dan trapesium, jika belum paham silakan bertanya pada bp/ibu guru kalian.

Untuk menguji pemahaman kalian, cobalah kerjakan soal berikut,

LATIHAN MANDIRI

BAB 8 BANGUN RUANG SISI DATAR (Menyelesaikan Masalah Kontekstual Yang berkaitan Dengan Bangun Ruang Sisi Datar)

 

BAB 8 BANGUN RUANG SISI DATAR 

(Menyelesaikan Masalah Kontekstual Yang berkaitan Dengan 

Bangun Ruang Sisi Datar)

Pada 3 minggu yang lalu kita telah belajar konsep bangun ruang sisi datar dari kubus, balok, prisma dan limas

Dari definisi, jaring-jaring, hingga konsep luas permukaan dan volumenya

Yuk kita ingat kembali

Hari ini kita akan belajar mengaplikasikan konsep-konsep di atas untuk menyelesaikan masalah kontekstual dalam kehidupan sehari-hari.

Kita akan langsung membahas beberapa permasalahan dari buku paket kalian

Contoh 1

Buku paket halaman 216 nomor 2

Disediakan kawat yang panjangnya 6 m, akan dibuat kerangka balok berukuran 13 cm x 9 cm x 8 cm. Banyak kerangka balok yang dapat dibuat dari kawat tersebut adalah …

a.    3 buah

b.    4 buah

c.    5 buah

d.    6 buah

Penyelesaian :

 Diketahui :

Panjang kawat = 6 m = 600 cm

Balok

p = 13 cm

l = 9 cm

t = 8 cm

 

Ditanya : Banyak kerangka balok

Jawab :

Kerangka balok = Jumlah panjang rusuk

    = 4 x (p + l + t)

                       = 4 x (13 + 9 + 8)

                       = 4 x 30

                       = 120 cm

Jadi untuk membuat satu buah kerangka balok dibutuhkan kawat sepanjang 120 cm

 

Kawat yang tersedia 6 m = 600 cm

Maka banyak kerangka balok yang dapat dibuat = 600 : 120

                                                                    = 5 buah

 Jawab : c

Contoh 2

Buku paket halaman 218 nomor 16

Halimah akan membuat model balok padat yang terbuat dari bahan gypsum dengan luas alas 200 cm2 dan tingginya 9 cm. Harga gypsum per liter adalah Rp15.000,-. Rupiah minimal uang Halimah yang harus dikeluarkan untuk membuat model balok adalah …

a.    Rp18.000,-

b.    Rp24.000,-

c.    Rp27.000,-

d.    Rp34.000,-

Penyelesaian :

Diketahui :

Balok

Luas alas = 200 cm2 = 2 dm2

t = 9 cm = 0,9 dm

(karena 1 liter = 1 dm3 maka satuannya kita jadikan dm dahulu, agar lebih mudah)

Harga gypsum per liter = Rp15.000,-

 

Ditanya : Rupiah minimal uang Halimah yang harus dikeluarkan untuk membuat model balok

Jawab :

Luas alas = 200 cm2 = 2 dm2 artinya p x l = 2 dm2   

Jadi untuk membuat model balok diperlukan gypsum 1,8 liter

Harga gypsum per liter = Rp15.000,-  

Maka rupiah minimal uang Halimah yang harus dikeluarkan untuk membuat model balok = 1,8 x 15.000

= 27.000

Jawab : c

 

Demikian 2 contoh pembahasan tentang masalah kontekstual dalam kehidupan sehari-hari

Semoga bisa kalian pahami dengan baik

Intinya kalian harus memahami soal dengan baik, menganalisa hal-hal yang diketahui dan ditanyakan dan kemudian menyusun strategi penyelesaiannya berdasarkan konsep yang sudah kalian pelajari

Dan sering-seringlah berlatih

Dengan semakin sering berlatih, semakin luas wawasan kalian dan semakin lihai kalian dalam menyelesaikannya

SEMANGAT …

Selanjutnya yuk berlatih menyelesaikan permasalahan di bawah ini

Silahkan berdiskusi dengan teman

Selamat berlatih, sukses selalu ...

 

LATIHAN

Andi akan membuat sebuah kerangka Balok yang memiliki ukuran 50 cm x 30 cm x 20 cm. 

a. Berapa meter panjang kawat yang dibutuhkan untuk membuat 1 (satu) buah kerangka balok ?

b.Hitunglah panjang kawat yang dibutuhkan Andi untuk membuat 5 (lima) kerangka Balok !

c. Berapa minimal uang yang dikeluarkan Andi jika harga 1 m kawat = Rp 9.000,-